Copyright (c) 2001 by the Space Frontier Foundation. All rights reserved.

[Original word document also available online.]

Abstract

Over 5,000 tons of junk in orbit around the Earth cost billions and billions to launch. This debris should be salvaged and serve as ballast for a Low Earth Orbit (LEO) tether. Such a tether can double the payload delivered by an orbiter to LEO. Used as a junk man's ladder, this tether can forward payload to the Moon’s orbit, cutting the total mass to support a Moon mission in half. Design of a junk collector to retrieve 5 to 10 ton pieces of junk will make these savings plausible.

Tethers are an attractive option in space flight because they can accumulate energy gradually, and release it to toss a payload. An Electrodynamic Tether (EDT) can use electricity to push against the Earth's magnetic field to climb or to replace orbital energy from a payload catch or toss. Using such an EDT to gather some junk for ballast for the ladder would be cheaper than launching mass from Earth. A junk collector design based on a 20-km tether powered by 80 kW of solar cells is proposed. Using junk for ballast, the LEO tether could be built for a mass investment of 140 tons launched to orbit. This "Junk Man's ladder" can lift 10 tons every six days from LEO and send it to the Moon, with 1MW of solar cells.

Tethers

Tethers (two objects in orbit connected by a wire) have exciting potential for frequent flyer miles. In the simple case, the two masses will hang so that the wire points to the center of the Earth. Thus we have one mass in a low “orbit”, moving slower than local circular velocity, and the other mass in a high “orbit” moving faster than the local circular velocity.

For simplicity, this review will assume circular orbits. Tethers can be in an ellipse; those are just more complicated to discuss.

The two connected objects will move at the orbital velocity of their center of mass. If they have unequal masses, the lighter end will be farther from that center of mass than the heavy end. The distance from the center of mass determines the energy that can be given to either object by a toss. If the wire is cut, or released, the two masses will separate and follow a pair of ellipses. The high mass will be in a ellipse whose low point (perigee) is the location of the release, and whose high point (apogee) will depend upon the length of the tether and the ratio of this mass to the combined mass before the release.

If the heavy end has 10 times the mass of the light end, the light end will be 10 times farther from the center of mass. If this tether was 66 km long, the light end will be 60 km from the center of mass. Figure 1 shows this case. For short tethers, the tether toss adds about 6 times the distance from the center of mass to the ellipse that is the new orbit. If released, the light end would be in an ellipse that ranged from 60 km to 420 km from the original center of mass orbit. The heavy end would only be 6 km from the center of mass. When separated, the heavy end will range from 6 to 42 kilometers from the original center of mass orbit.

For lifting freight from the Earth to higher orbits, large mass will make most of the orbit change in the payload, with only minor changes to the orbit of the lifting station. If the heavy mass were 100 times the mass of the light end, in the example above, the light end would be 65.3 km from the center of mass. Then the heavy end will shift its orbit by 0.65 to 4.5 km.

For long tethers, calculating the new orbit is more complicated (its not just 6 times). The ratio of the masses remains an important consideration because it determines the distance from the center of mass to the payload.

Guidebook

Many of the calculations in this paper are based on the Guidebook for Analysis of Tether Applications; (Ref. #3) often referred to as the Guidebook in this paper.

Most of the numbers for an EDT are subject to variation. This is an elaborate back of the envelope exercise. Precision is not claimed.

Junk Man's Ladder

The ladder described here consists of a trapeze at the low end and a sling at the high end. There is also a large central mass, which will act as a flywheel to store kinetic energy for either end of the ladder. Payloads will be caught at the trapeze, and then carried up the ladder an appropriate distance and tossed outward. For a low catch or a high release, the flywheel will have to supply energy. For a low release or a high catch, the payload may put energy back into the flywheel.

The high end of the ladder is moving faster than the inertial mass (ballast) and acts as a sling to throw payloads to higher orbits. By using a large inertial mass, and a long tether, such a sling can slay Goliath sized problems. A payload tossed from the right point could be in an ellipse that reaches the orbit of the Moon or Geosyncronous Earth Orbit (GEO – a 24-hour or Clarke orbit).

The high end can catch a payload, but most of today's focus is on payload leaving Earth, so it will usually be called the sling end of the tether.

If the ladder is supporting traffic leaving Earth, it will have to replace the energy used to drive that traffic. This may be done if there is solar power that can drive an electric motor that uses the Earth's magnetic field as part of that motor.

Any mass can serve another use and also be valuable as ballast. This mass can be anyplace on the ladder, only the center of mass needs to be at the right altitude. Hotels or low gravity industry can be served by the ladder and add to the ballast. Variable apparent gravity is available. Low gee environments exist near the center of mass. The trapeze end provides 20% of gravity. Industry that needs low gravity can pick any level they want.

A hotel at 400 km altitude would have an apparent gravity (local gravity offset by centripetal force) of about 11% of earth standard gravity. High enough to keep things in place and provide orientation but low enough to be a novelty. Hotels that can tolerate occasional jerks, (and most can) could do double duty as ballast for the tether.

Illustrating some Tosses

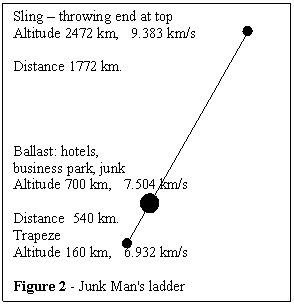
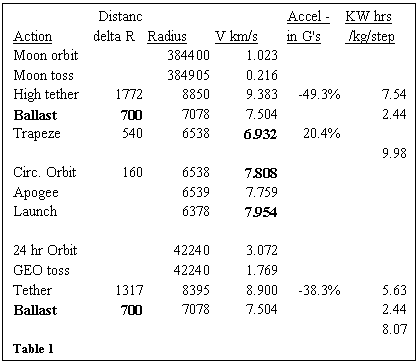
Figure 2 and table 1 display some information about a tether with center of mass at 700-km altitude. This seemed to be high enough to lower the trapeze velocity, but stay under the Van Allen belt. At this altitude, circular velocity is 7.504 km/s.

The first 5 rows in table 1 display data about the use of this ladder for sending payload to the Moon. The trapeze has a length of 540-km (making it 160 km above the Earth). The (sub-) orbital velocity is only 6.932 km/s. Something standing or hanging on the trapeze would have a net acceleration of about 20% of Earth gravity. It would require 2.44 kW hours to raise a kilogram from the trapeze to the center of mass.

The sling or tossing end has a length of 1772 kilometers (the total length of the ladder is 2312 km). This sling must move at 9.383 km/s to keep up with the center of mass. Released from this radius, the ellipse touches the orbit of the Moon (384,400-km), with a slight excess. Ignoring the Moon, an additional velocity change (or delta V) of 0.8 km/s would be needed to circularize the orbit. The gravity of the Moon makes this interesting, but useless data. Note that prior to release, the payload would have a net centripetal force of almost half the gravity on Earth.

Raising a payload from 160-km altitude to 2472-km altitude can be done with an elevator or maglev motor. It would take 9.98-kilowatt (kW) hours of energy to move one kilogram from the trapeze to the top of this ladder. In California, when we can get kW-hours, we have been paying about 10 cents for one. That translates to about $1 per kg, or $0.45 per pound. Using launch cost assumptions later in this paper, LEO solar-cell kW-hours cost 25 cents, so the cost is closer to $2.5 per kg. The energy at the trapeze is less than half the energy at the sling. (The orbiter supplies 7.07 kW-hours per kg.)

The Orbit, Apogee, and Launch (rows 6-8 in table 1) were an effort to estimate the velocity a conventional orbiter needs to get into a 160-km altitude orbit. The launch velocity (7.954 km/sec) produces an ellipse whose apogee is at an altitude of 160 km. Circular orbit velocity is 7.808 km/sec, so the orbiter needs an additional 0.05 km/sec (or 50 meters/sec) of delta V. The trapeze end of the ladder is moving at 6.932 km/sec. A more eccentric ellipse that reaches 160-km altitude with a velocity of 6.932 km/sec needs only 7.242 km/sec at the surface of the Earth.

These numbers ignore atmospheric losses and the boost from the rotation of the Earth. If we were in an equatorial orbit, the rotation of the Earth would add 0.464 km/sec – so an equatorial launched rocket only needs to supply 6.778 km/sec to catch the trapeze. By contrast, a simple equatorial launch would reduce the 7.808 km/sec to a relativistic 7.563 km/sec.

The trapeze reduces the rocket delta V from 7.56 km/sec to 6.78 km/sec, saving 0.78 km/s. Putting these two numbers in the rocket equation gives an estimate of the larger payload: between 2 and 2.5 times the original payload.

Non-equatorial launches have higher velocity costs. A launch from Las Vegas would only get a boost of 0.375 km/sec. Cape Canaveral still has 0.408-km/sec rotational boost. An equatorial launch is the optimum, but we have been living with lower assists for 40 years.

Rows 9-12 in table 1 look at a toss to GEO. The circular velocity at GEO is calculated first. A release from 1317 km above the center of mass follows an ellipse that reaches to GEO. An additional delta V of 1.3 km would be needed to convert to circular velocity of 3.072 km/s. At the 1317-km point, the ladder is moving at 8.9 km/s. The apparent gravity would be 38% of Earth normal (centripetal force up is greater than local gravity). Climbing the ladder from the trapeze to 1317 km above the center of mass costs 8.07-kilowatt hours. This ladder can support solar power satellites or communications satellites as well as Moon traffic.

Another interesting “toss” is at a sling length of 1173 km, when the payload ellipse reaches 31,450 km. This is interesting only if there is another ladder at GEO with a trapeze length of 10750 km. This GEO ladder, with a sling length of 8805 km, would forward payloads to the Moon. Some of the cleanup junk could be tossed toward GEO, to serve as inertial mass for the second tether.

Two cooperating tethers probably need to be in equatorial orbits. Orbits that cross the equator get a torque that moves the plane of the orbit. The rate of change is different for different altitudes above the Earth. It would be difficult to keep two tethers in the same plane, unless they orbit over the equator.

Two such tethers would form a conveyer belt; the payload will take weeks to get from LEO to the release from the GEO tether. This combination reduces the demands on the LEO tether. It only takes 7.48 kW hours to lift 1 Kg to 117k km. The remaining 2.5 kW hours for the Moon can be supplied at GEO, where the sun is always up. Unfortunately, it takes building two tethers, so will not be discussed in detail.

Hazards

Unfortunately, the rosy picture just described has some brutal facts that appear to put it out of reach.

The first brutal fact: at current and projected launch costs, putting a large inertial mass (ballast) into orbit is prohibitively expensive.

Second brutal fact: there is an erosion problem due to interplanetary dust falling to the Earth. These are mostly very small particles, which will pit and erode a tether. A wire has an expected lifetime that is a function of the diameter of the wire. The assumptions are that there is some excess strength designed into the wire that can survive erosion by dust, but that the wire will eventually be cut by a larger particle. For individual wires or strands of a complete tether, the micrometeorite hazard is important.

Third brutal fact: for tethers over 10-mm diameter, the risk of impact with debris (junk) becomes larger than the risk due to micrometeorites. There are about 700 pieces of junk (with mass greater than 5 tons each) in orbits between 900 and 4000 km altitude.

On page 27 of the Guidebook, there is a calculation that an Earth-based Space Elevator would expect about 1.2 cuts per year due to the debris orbiting less than 4,000 km above the Earth. The ladder discussed in this paper reaches between 160-km and 2500-km altitudes. It would face the same risk of cuts.

There has been much worry about the hazards implied by this junk. Often it is suggested that it be de-orbited. I have assumed that it can be treated like abandoned property. Using maritime conventions, whoever collected it would have salvage rights. There may be some pieces that are still claimed. In this case, a recovery fee should be negotiable.

Sometimes two problems can create a solution. If we can gather this junk to a useful orbit, we can provide the ballast mass for a junk man's ladder and remove the hazard of crossing orbits with said junk.

Principles of a space junk collector.

Since we started with tethers, it will be natural to look at an electrodynamic tether (EDT) as a junk collector. An EDT is a simple motor that drives a current in the Earth's magnetic field to generate thrust while in orbit near the Earth.

The collector will match orbits with some piece of junk. Then the junk collector will tow that junk to the 700-km foundation orbit. Since the junk is in higher orbits than the collection orbit, the junk collector climbs to a higher orbit when empty, and is coming down (to a lower orbit) when loaded.

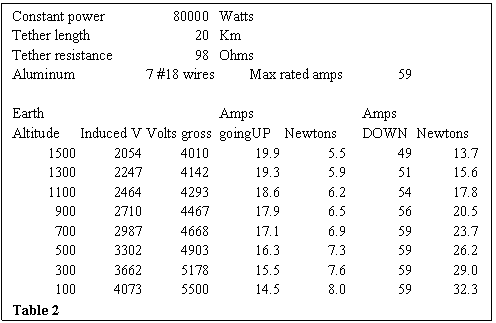
Table 2 displays information for a 20-km EDT at various altitudes. It also displays the optimal voltage and current at these altitudes for 80 kW of solar cells. The induced voltage for a 20-km wire is shown. This is calculated from page 31 of the Guidebook as volts per kilometer = 215 * (radius Earth/radius orbit)^3.5. This assumes local circular velocity. When we are climbing to a higher orbit, this voltage works against the power supply. Fighting this voltage makes it hard to get very many amps.

The voltage that optimizes the number of amps is shown in column 3, and the maximum amps in column 4. Amps are converted to Newtons by another equation on page 31 of the Guidebook: Newtons per (amp * Km) = 0.029 * (radius of the Earth/radius of the orbit)^3.5. This has the same relation to radius and the same circular velocity assumption.

For the downhill (return) part of the retrieval, the amps are the sum of the induced voltage working through the tether resistance and the 80 kW driving current through the same resistance. This is displayed in columns 6 and 7 of table 2.

Another way to say this is that coming down an EDT can get current by trading altitude for thrust. The junk collector can get 2.5-4 times the thrust when the voltages add relative to when they work against each other. Thrust to lower the orbit can happen at night, not just while the sun is powering the solar cells. Night power will not get as much thrust as the combination of induced voltage and the 80 kW plant.

Coming down, an 80 kW solar cell array can drive 28 amps through 98 ohms (this is independent of altitude). A voltage of about 2800 volts would be required for this part of the trip.

When an EDT junk collector starts to climb from 700-kilometer altitude to 1000 km, it will convert the circular orbit to an ellipse that touches the original orbit and something close to the goal. This happens because power is available only during the sunny part of the orbit. For this ellipse, the velocity will be higher at perigee than local circular velocity (and lower than circular velocity at the apogee). A more accurate force calculation would need iterations and more complexity than table 2. These tables are still useful; the circular and elliptical velocities are within 5%.

The limit on force down may be the maximum safe current that the wire can carry. Table 2 has an entry “Max rated amps” which is the recommended maximum current for house wiring. At 800-km or lower altitudes, this table shows that the downward force is limited by this maximum.

The conductor that completes the circuit with the ionosphere may limit the current. The design relies upon the bare wire conductor mentioned in ref. 4. Bare wires make good electron catchers in the ionosphere.

Even though more amps are available at 1500-km altitude, the total force is less, since the magnetic field is weaker. The force is greater than would come from constant amps. Variable voltage and variable current are attractive, if they don't cost too much mass.

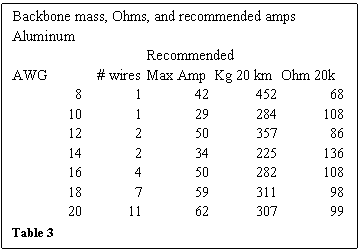
Mass, ohms, Current

Mass, ohms and amps are input for table 2. Rationalization for selected numbers follows.

Values of recommended maximum amps are available for Copper (Cu). Since Cu is 3.3 times as heavy as Aluminum (Al), Al seems an easy choice for space applications. There is a guideline that Al limit current to 84% of the Cu numbers (Ref. 2).

The ohms listed in table 3 are for a particular temperature, 20 Centigrade (68 F). Copper had two values, resistance at 0 C and 50 C, with about a 25% reduction at 0 C relative to the resistance at 50 C. In general the resistance is lower when the temperature is lower. Since the black body temperature at the Earth’s orbit is about 0 C, the tendency is for things to be a bit cool (remember Tom Hanks in Apollo 13).

A graph on page 9 of the Guidebook shows tether temperatures ranging from 180 K to 260K at 500-km altitude orbit. Resistance will be less at these temperatures than used in these tables. I.e. we should get more amps than calculated.

Fail-safe

Any structure in space faces some hazard due to micrometeorite impact. Formulas in the Guidebook calculate the probability of damage to a tether.

A basic EDT tether could use #10 aluminum wire. The recommended maximum current for #10 Al wires is 29 amps. This is plenty for climbing, but limits lowering of junk. This diameter wire has an expected lifetime of about 216 days. The 20 km of #10 wire would mass 284 kg.

Several smaller wires in parallel can increase the maximum current. We will also reduce the failure rate if we have several wires in parallel and are prepared to repair breaks.

From a mass, current, and ohms analysis, 7 wires of #18 AWG aluminum wire is a better choice. The recommended maximum current is doubled, the mass is 11% more (311-kg), and the resistance is less.

Cross connectors will space these wires 5-mm apart, so the result is a ribbon cable, 31 mm wide (about 1.25 inch). With these conductors connecting them every 10 meters, a failure will be limited to the loss of 10 meters. Most of the time, we could repair a break by clamping a connector to the broken ends. A repair robot to gather the cut ends and apply a clamp-on connector seems simple and practical.

The hazard calculation says that with a 20-km length of #18 wire, I could expect a cut every 19 days. With 7 wires, each will expect a break in 19 days; one of them will break about every 2.7 days! If we can repair a break in less than a day, the breaks will be a nuisance, not a catastrophe.

There is still some risk of a catastrophic break that would isolate some power units. To guard against this, the segments should be programmed to return to the collection orbit for more serious repair. With power disbursed, each segment should have enough power to move itself. If the failure occurs while hauling junk to the collection area, the power to mass ratio could be discouraging (and we would need to send out another junk collector to help).

For safety, the segments should probably aim at an orbit that was ahead (or behind) the base a few kilometers, but in the same orbit as the base.

The main tether also needs a fail-safe model. The preliminary model used six strands of Kevlar, separated to reduce the risk of simultaneous failures. A maglev would run up and down a pair of them. If there is a platform every 100-km, breaks will be isolated. A quick hazard calculation gave one of these braking every few days. An ongoing maintenance program is necessary for tether survival in LEO.

Model A – building a space junk collector.

The classic Model A was always breaking down, but could be repaired with bailing wire (this was before duct tape). We need that kind of design for a junk collector.

This model A space junk collector is built on a 20-km flat cable. Each end has 3 kilometers that are bare; the central part of the wire is insulated. The bare wire exchanges electrons with the ionosphere. When climbing the lower bare part of the wire is collecting electrons and the upper bare section is sending them off. This concept was published in Ref. 4. The roles are reversed coming down.

The 20-km of 7 #18 AWG aluminum wire would weigh 311 kg. The cross wires every 10 meters add less than a kilogram. The robot to repair broken wires should add 10 kg or so. A supply of 10-meter replacement wires would add another kg. A robot arm to catch and attach the junk should add 20-30 kg.

There are 4 propulsion units on the insulated part of the wire, each providing 20 kW of solar cells. At 250 w/kg, the solar cells mass 80 Kg. At 1 kW per 4 meters^2, that would be 80 m^2. For symmetry, we use 2-5x8 meter arrays. They need orientation and movement to keep the cells facing the sun.

Each unit is able to control the direction (up, down, and off) of electricity to interact with the Earth’s magnetic field. The box also needs resistance or some way to get only partial current coming down. Each unit operates independently. They use the conducting wires between them for communication. They need radar or some vision mechanism for final approach. They need sun location, earth location, and enough computation to keep track of where they are, and where they want to be. Radio communication with a ground control allows selection of targets and other assistance to the junk collector.

Bare wire can make a circuit with the ionosphere, which will cause drag. A motor to reel in the bare wire by the end units can reduce drag. To get just enough electrons, the amount of exposed bare wire would be adjusted.

As a safety feature, each unit also has a bare wire flat cable that can be extended if they need to gather electrons locally. This is only used if they are separated, when the remnants can maneuver home.

About 60-70 Kg seemed reasonable for the rest of a unit. This brings the total mass of the garbage collector to about one ton.

The 80 kW of solar power will drive the one ton EDT uphill (to higher orbits) at an acceleration of about .6 cm/s^2. Using the energy of the higher orbit, it can bring a 5 ton payload to lower orbits at accelerations of about 0.3 cm/s^2.

Foundation for a ladder – the first rungs.

Every ladder needs a firm base to rest upon. This ladder will use ballast (inertial mass) at 700-km altitude as its foundation.

This paper assumes orbiters with payloads of 2-5 tons, with a gross mass to LEO of 15-25 tons. A trapeze to catch larger ships would require a heavier tether.

The first stage in construction is to hang a trapeze from the 700-km altitude that can be used to reduce the cost of launch. From page 25 of the Guidebook, we get that Mt/Mp (mass of tether over mass of payload) is = (Delta V) / (k * Vc). The trapeze has a Delta V of 0.57 km/s. For hanging tethers, k is 1.15. The characteristic velocity of Kevlar (reading from a graph) is about 0.8. This gives Mt/Mp of 0.39. We need 9.7 tons of Kevlar tether to catch a 25-ton orbiter and payload.

Spectra 2000™ has a characteristic velocity of about 1.5. This would give Mt/Mp of 0.11. With this, we should be able to catch a 25-ton payload with 3 tons of tether.

If we can separate payloads and catch them without catching the entire orbiter, we need about 2 tons of Kevlar to start a trapeze. Catching payload is about as difficult as catching a baseball – the relative speeds at catch are only a few kilometers per hour. It might be hard to catch 2-5 ton baseballs.

If that seems worrisome, and we want to have the orbiter able to maneuver to the trapeze, we need about 10 tons of Kevlar to start a trapeze.

We also need some solar power plant, say 100 kW for a start. This 100 kW will have a dual purpose, to lift payload from the trapeze to the center of mass, and to drive an EDT to compensate for energy lost when payload is caught. Since one purpose is to drive an EDT, this power plant is several of the 20 kW units used in the junk collector, and could carry itself from a 160-km orbit to the 700-km altitude orbit.

Assemblers to sort junk and assemble the tether would complete the initial cargo. Other cargo that will be needed at the ballast dump is tie-downs, to hold the collected junk. This gives an initial package of 15-20 tons at 700-km orbit.

We start by creating a ballast dump at an altitude of 700 km. Send out a fleet of space junk collectors. Since they need to climb from a nominal 160-km orbit past the 700-km altitude, they could haul some freight that far. They each weigh about a ton. These junk collectors are weak going uphill with cargo, but they could deliver 1 or 2 tons from a 160-km orbit to the 700-km orbit in 4 to 5 days.

There is an interesting option when the cargo includes tether segments. If we have the flexibility to use them at separation from the orbiter, we can shorten the delivery time. Remember in the tether review that a short tether will add 6 times the distance to the center of mass to the tossing ellipse.

If the orbiter weighs 3 times as much as the cargo, then it will sink below the center of mass 1/3 as much as the cargo rises above. If we can reel out 80 km of tether, we’d start 60 km above the center of mass. Apogee would be about 420 km above. If we start at 160 km, the apogee is at 580 km. The orbiter will fall 140 km, which should de-orbit it (and save rocket fuel to slow for the de-orbit).

The first targets would be junk in lowest orbits (closest, and don’t want to go through these orbits getting something else). Targets would be selected from pieces whose orbits are tracked. Finding an orbital plane near the current ballast collection orbit would be an important saving.

For the first junk collected, a round trip should take about 3 days. In 30 days we expect to get 50 tons from one junk collector. If we have heavier junk, the time is slightly longer, but the payoff is higher tonnage per day. The tether Guidebook said there were 700 tracked pieces of junk over 5 tons each. If they total 6,000 tons of mass, they would average 8.5 tons each.

We can use a sling to toss a junk collector so it gets back to the debris orbits faster. Since the junk collector mass is about 1 ton, we can start as soon as we have collected even a few pieces into the ballast orbit. We can toss the junk collector back toward the debris, which reduces the climb time. If rendezvous and catching become routine, we could catch an incoming payload with savings of energy and time (use the tossing tether as a trapeze). The junk collector just needs to tow the junk into an elliptical orbit that is tangent to the tether orbit. If this works, matching the orbital plane is the hard part of the retrieval.

Hotels, business parks welcome.

When we gather 1000 tons (or so) at the 700-km orbit, and hang a trapeze from it, we can start catching payload. This multiplies the payload an orbiter can deliver by 2-2.5. If we figure a fixed cost per flight, then this should cut the cost per pound of payload by a factor of 2.

This price should make the ladder very attractive to hotels or low gravity industry. If between the ladder and the orbiter we charge 60% of delivery to LEO, we should get market share and have more business than we can handle.

It takes about 2.5 kW hours to raise one kg from 160-km to 700-km. A 1-ton payload would need 40 hours with the 100 kW solar cell power plant. Clearly one of the first payloads is more power. Now it is cheaper to build up a solar cell array to lift cargo faster and develop any low gravity industry we can fit into the ladder.

NASA has a goal to cut launch costs to $1000 per pound in the next few years. If this happens, and a tether can double the payload of an orbiter, it will cut the cost per pound to $500/lb to LEO. As a bonus, we have payload at 700-km, not 160-200 km altitudes. This is interesting, because several studies have claimed that when the cost to LEO drops below $600/lb, commercial use of space explodes.

If G. Harry Stine was right, costs should come below that as the market grows with airline style operation (Ref. 5). With an airline model, traffic increases lead to further price declines. The fuel cost to launch is under $40/lb, energy is not the problem. Frequent flights will pay off the investment in an orbiter at a lower cost per flight.

Draw bridge

There is other traffic in LEO (we assume the ISS will survive). This should mean that the trapeze would occasionally be raised to clear that space. Orbits are predictable, so we can anticipate the need, and when it is safe to lower the trapeze again.

Final Construction

For the 1.8 KM/sec delta V that the toss to the Moon represents, the mass of a Kevlar tether is 11x the mass of the payload. If we want to toss 10 ton payloads, we need 110 tons in the tossing tether.

After the lower tether is constructed, the additional parts can be launched to a trapeze, and lifted by ladder operations. The launch cost for the upper segments of the ladder should be half price ($500/lb). Another 110 tons at this price costs $110 M.

To build the ladder, start with 10 junk collectors, at one ton each. An additional 20 tons to hold the initial junk and build the low tether need to be launched at full cost. This would be $60 M. This makes the launch cost of the ladder about $170 million.

With Spectra 2000™, the initial mass is 15 tons, (plus collectors) for a launch cost of $50M. The upper segments would only need 25 tons to toss 10 tons, for an additional $50M. With this model, the total launch cost to build a Junk Man's ladder is $100M.

Payoff

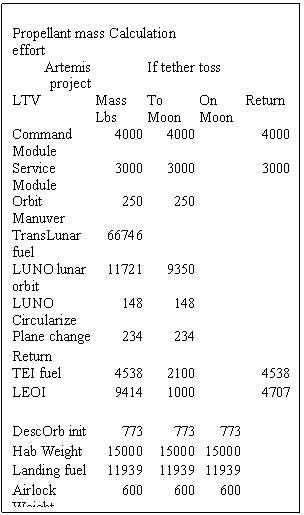
To illustrate the payoff from this effort, let us look at the Artemis project reference mission. This project has published plans for assembling a Lunar Transfer Vehicle in LEO (at 100-mile altitude). This LTV takes a lunar base to the Moon, where a small crew spends two weeks in a part of Mare Angus. They would collect samples and return about 700 pounds to Earth.

The mass assembled in LEO is 130,993 lbs. The first two columns of table 4 gather data from their web page. (The only point is that fuel is a huge part of the mass.)

Column 3 itemizes savings with the Junk man's ladder. We can reduce the mass launched to LEO from 65.5 tons to 25.1 tons. This comes by eliminating 33.4 tons of fuel for the trans-Lunar orbit insertion. We also reduce the return LEO insertion fuel by 4.2 tons (we leave some fuel to rendezvous with the sling end of the ladder). Since the payload to the Moon is 4.2 tons less, we can save 1.4 tons each for the Lunar Orbit Insertion, and the Transearth Injection. About 60% of the mass launched into LEO is fuel that the ladder can replace with a sling or a catch.

The following argument assumes that the cost of launch to LEO is the dominant cost of a Moon trip. NASA has a goal to cut launch costs to $1000 per pound in the next few years. For convenience, assume constant launch costs of $1000 per pound. For current launch costs, just multiply by 10 or 12. The savings are even more impressive.

The trapeze act at LEO should cut launch costs in half. The mass needed at LEO has been cut to 40%. This is offset by the electricity cost to climb the ladder, which is only $2.50 per kilogram.

Using the NASA goal, the Artemis project would cost $131 Million in launch costs. With an orbiting ladder, we only need to launch 26 tons. With a trapeze, the launch cost per pound is cut in half. At $500/lb, the launch cost for this mission is $26M.

With Spectra 2000™, the cost of the junk man's ladder and the Artemis project is about the same as the cost of the Artemis project without a ladder.

If we intend to exploit the Moon, make frequent trips; the investment in a ladder will pay off. A free flying junk collector to gather ballast makes it easy and cheap to re-cycle orbital junk. With orbital junk for ballast, a LEO tether is not too expensive, and seems an attractive path to the Moon.

Halfway to anywhere

Robert Heinlein is often quoted, "Reach Low Earth Orbit, and you are halfway to anywhere in the solar system". This junk man's ladder could complete the Heinlein quotation, and give us the other halfway to anywhere in the solar system.

Bibliography

1. R. Moss & M. Martinez-Sanchez, Extending the Operational Altitude of Solar Sails Down to Space Station Altitudes with an Electrodynamic Tether. SSI conference #8, 1991. Pages 159-174

2. Handbook of Chemistry and Physics, 1991-2 edition. Wire tables, pages 15.25-15.29

3. Joseph A. Carroll, Guidebook for Analysis of Tether Applications. March 1985, final report for contract with Martin Marietta Corporation. PDF available at www.tetherapplications.com - recommended.

4. L. Johnson, R.D. Estes, E. Lorenzini, M. Martinez-Sanchez, J. Sanmatin, I. Vas, Electrodynamic Tethers for Spacecraft Propulsion. AIAA 98-0983, 1998.

5. G. Harry Stine, Halfway to Anywhere. 1996

Junk Man’s Ladder, a path to the Moon